优化——闭环时本质图优化

本章节主要阐述在ORB-SLAM2系统中，当检测到闭环（Loop Closing）后，如何通过优化一个称为“本质图”（Essential Graph）的结构来全局校正和优化所有关键帧的位姿。这个过程对消除累积误差、提升地图全局一致性和定位精度至关重要。

一、优化的核心目标与对象

• 核心函数：OptimizeEssentialGraph。
• 主要目标：在闭环确认后，对系统中所有已记录的关键帧的位姿（包括位置和姿态，即Sim(3)变换）进行一次全局性的优化调整。
• 关键点：
  • 不直接优化地图点：在这一特定步骤中，优化过程的变量是关键帧的位姿，而不是三维地图点的坐标。地图点的位置会在关键帧位姿优化完毕后，根据其参考关键帧的位姿更新进行调整。
  • 全局性：优化会影响到地图中所有的关键帧，以达到全局最优的目的。

二、本质图的构成：顶点 (Vertices)

在本质图优化这个图优化问题中，“顶点”代表了需要被优化的实体。

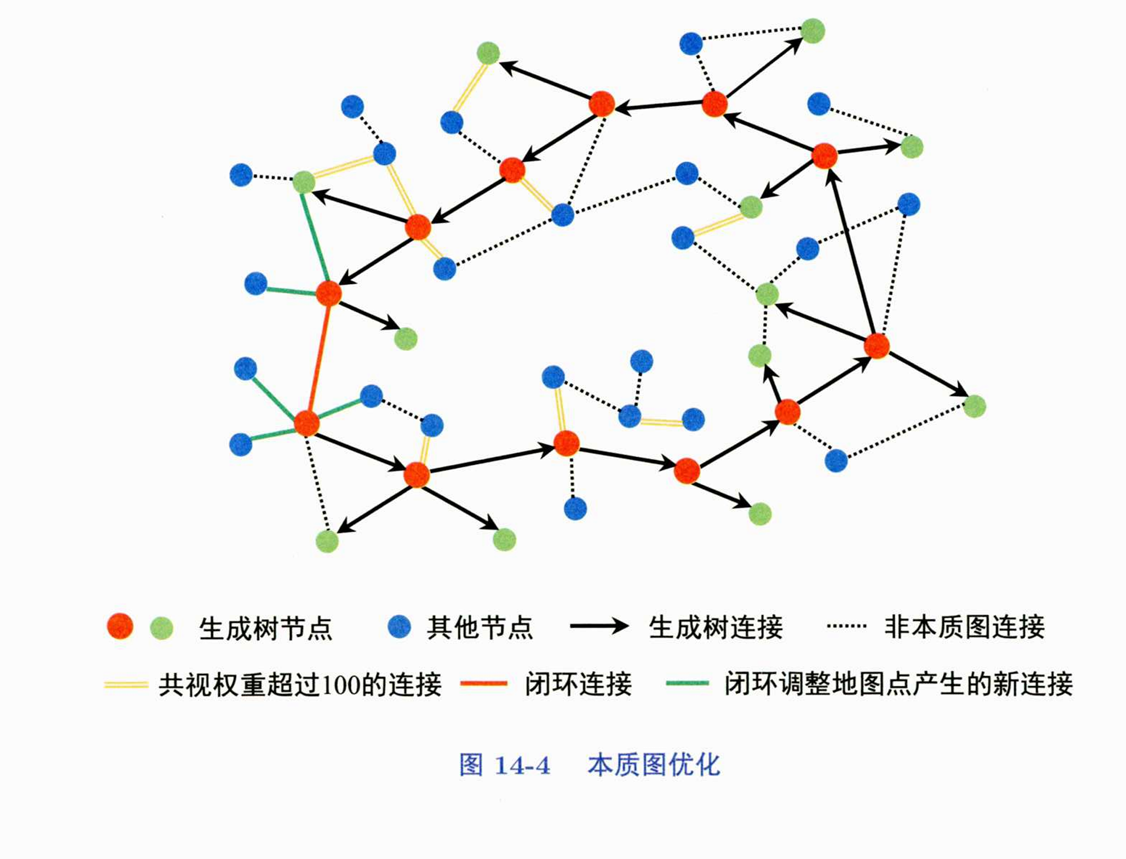
• 定义：每个顶点对应一个关键帧的位姿。可以参考书中的图14-4，图中的每一个节点（无论是红色、绿色还是蓝色）都可视为一个顶点。

• g2o类型：在g2o中，这些顶点的具体类型被定义为 g2o::VertexSim3Expmap。

  • Sim(3)变换：Sim3代表相似变换（Similarity Transformation），它包含了旋转（3自由度）、平移（3自由度）和尺度（1自由度）三个部分，共7个自由度。这意味着优化不仅会调整关键帧在三维空间中的位置和朝向，还可能调整它们之间的相对尺度因子。
  • 尺度优化选项：g2o::VertexSim3Expmap 类型顶点的一个特性是，它可以根据实际使用的传感器类型（如单目相机、双目相机或RGB-D相机）来决定是否将尺度因子作为优化变量。对于单目SLAM，尺度是不确定的，因此在闭环时通过Sim(3)优化可以恢复全局尺度；而对于双目或RGB-D相机，尺度是可测量的，通常会固定尺度为1。

  

三、本质图的构成：边 (Edges)

“边”在图优化中代表了顶点之间的约束关系或测量。

• 定义：边连接了两个关键帧顶点，表示它们之间存在某种几何约束（通常是相对位姿变换）。
• g2o类型：尽管边的来源和意义有所不同，但在本质图优化中，它们的数据类型统一为二元边 g2o::EdgeSim3。
• 边的主要类型（参照图14-4）：
  1. 闭环相关的连接关系：
     • 闭环调整后新增的连接（图14-4中绿色的连线）：当闭环发生后，会进行地图点的融合和调整。这个过程可能会使得一些原本没有直接共视关系或者共视关系较弱的关键帧之间，因为共享了融合后的地图点而产生新的、较强的连接关系。这些新的连接会作为边加入到本质图中。
     • 形成闭环的直接连接（图14-4中红色的连线）：指当前关键帧（检测到闭环的帧）与它在历史轨迹中匹配到的那个闭环关键帧之间的直接连接。这是最核心的闭环约束。
  2. 生成树（Spanning Tree）连接关系（图14-4中黑色带箭头的连线）：ORB-SLAM2在跟踪过程中会维护一个关键帧的生成树（或称为共视树）。树中的边连接了具有较强共视关系的关键帧，通常是当前关键帧与其父关键帧（共视程度最高的关键帧）之间的连接。这些边构成了关键帧位姿图的一个基本骨架。
  3. 高共视权重（Covisibility）的连接关系（图14-4中黄色的双股连线）：除了生成树的边和闭环边之外，如果两个关键帧之间存在非常好的共视关系（例如，它们共同观测到的地图点数量超过一个设定的阈值，书中例子是至少100个），即使它们不是父子关系或直接的闭环关系，它们之间也会添加一条边。这增加了图的冗余度和鲁棒性。
• 边的筛选：书中提到，与完整的共视图（Covisibility Graph，包含所有共视关系）相比，本质图会有选择地移除一些连接关系（如图14-4中黑色的虚线所示）。这样做是为了在保证优化效果的前提下，减少图中边的数量，从而降低优化问题的复杂度和计算量，以加速优化过程的收敛速度。

四、边的误差定义（代价函数）

每条边都会贡献一个误差项到总的代价函数中，优化器的目标是最小化所有误差项之和。

• 边的测量值 (Measurement)：对于一条连接关键帧 $K_i$ 和关键帧 $K_j$ 的 g2o::EdgeSim3 边，其“测量值”通常表示从 $K_i$ 到 $K_j$ 的相对Sim(3)变换，我们记作 $S_{ji}$ (即 $T_{jw_i}$，从i坐标系到j坐标系的变换)。这个测量值是根据它们之间的共视地图点或者其他匹配信息计算得到的。
• 误差计算：
  • 设 $v_1$ 为关键帧 $K_i$ 的顶点，其当前估计的世界位姿为 $S_{iw}$ (从世界坐标系到 $K_i$ 坐标系的Sim(3)变换)。
  • 设 $v_2$ 为关键帧 $K_j$ 的顶点，其当前估计的世界位姿为 $S_{jw}$ (从世界坐标系到 $K_j$ 坐标系的Sim(3)变换)。
  • 根据当前的位姿估计，从 $K_i$ 到 $K_j$ 的相对位姿可以计算为 $S_{ji,est} = S_{jw} \cdot S_{iw}^{-1}$。
  • 书中给出的误差定义是 error_ = C * v1->estimate() * v2->estimate().inverse()，这里的 C 就是边的测量值 $S_{ji}$ (书中可能是符号约定，通常相对变换是 $S_{ji}$，而顶点估计是 $S_{iw}$ 和 $S_{jw}$，则误差通常形式为 $S_{ji} \cdot S_{jw} \cdot S_{iw}^{-1}$ 或者 $S_{ji}^{-1} \cdot S_{iw} \cdot S_{jw}^{-1}$，目标是使这个乘积接近单位阵)。更直观的理解是，我们希望测量得到的相对变换 $S_{ji}$ 与通过当前估计的世界位姿计算出的相对变换 $S_{jw} \cdot S_{iw}^{-1}$ 尽可能一致。
  • 误差可以表示为：$E_{ij} = S_{ji} \cdot (S_{jw} \cdot S_{iw}^{-1})^{-1} = S_{ji} \cdot S_{iw} \cdot S_{jw}^{-1}$。优化目标是使这个 $E_{ij}$ 尽可能接近单位Sim(3)变换。
  • 对数映射 (Logarithmic Map)：为了便于优化算法（如高斯牛顿法或列文伯格-马夸尔特法）处理，这个Sim(3)形式的误差会通过对数映射 _error = error_.log(); 转换为其对应的李代数向量（一个7维向量）。优化器会在这个李代数空间进行迭代更新。

简单来说，优化器会不断调整所有关键帧的Sim(3)位姿（即图中的顶点），使得通过这些位姿计算得到的关键帧间的相对变换，与图中边所代表的“测量到的”相对变换之间的差异最小。

五、本质图优化的完整流程

闭环时的本质图优化遵循一套明确的步骤：

1. 步骤1：构造g2o优化器
   • 初始化一个稀疏优化器对象（g2o::SparseOptimizer）。
   • 配置线性求解器（如 g2o::LinearSolverEigen）和块求解器（如 g2o::BlockSolver_7_3，因为Sim(3)位姿是7自由度，地图点是3自由度，但这里只优化位姿）。
   • 选择优化算法，通常是列文伯格-马夸尔特法（g2o::OptimizationAlgorithmLevenberg）。
   • 可以设置算法的一些参数，如初始Lambda值。
2. 步骤2：添加顶点到优化器
   • 遍历当前地图中所有的有效关键帧。
   • 为每个关键帧创建一个 g2o::VertexSim3Expmap 类型的顶点。
   • 设置顶点初始估计：
     • 优先使用在闭环过程中通过Sim(3)传播调整过的位姿（CorrectedSim3）作为该顶点的初始估计。
     • 如果某个关键帧没有经过Sim(3)传播调整（例如，它与闭环区域距离较远），则使用其在正常跟踪过程中得到的位姿（通常是SE(3)，尺度设为1.0来构成Sim(3)）。
     • 这些初始位姿会存储起来（如 vScw）。
   • 固定闭环匹配帧：将在闭环检测中匹配上的那个历史关键帧（pLoopKF）的顶点设置为固定（setFixed(true)）。这意味着在优化过程中，该关键帧的位姿不会被改变，它将作为整个图优化的绝对参考基准。
   • 初始关键帧的优化：值得注意的是，系统并没有固定地图的初始关键帧（第0帧），所以初始关键帧的位姿也会在这次全局优化中得到调整。
   • 尺度固定选项：根据 bFixScale 参数（通常由相机类型决定，如RGB-D或双目时为true），决定是否固定顶点的尺度因子（_fix_scale）。
   • 将创建的顶点添加到优化器中。
3. 步骤3：添加第一种类型的边（因闭环时地图点调整而新生成的连接）
   • 遍历 LoopConnections 这个数据结构，它存储了因为闭环后地图点融合而产生的新的关键帧间的连接关系。
   • 对于每一对新连接的关键帧 ($K_i$, $K_j$)：
     • 获取它们在步骤2中设置的初始Sim(3)位姿 $S_{iw}$ 和 $S_{jw}$ (从vScw中获取)。
     • 计算它们之间的相对Sim(3)变换 $S_{ji} = S_{jw} \cdot S_{iw}^{-1}$ 作为这条边的测量值。
     • 创建一个 g2o::EdgeSim3 类型的边，连接对应的两个顶点。
     • 设置边的测量值为计算得到的 $S_{ji}$。
     • 设置边的信息矩阵（information()），通常对于这类新增加的边，会使用单位矩阵，表示它们对总误差的贡献权重是均等的。
     • 将边添加到优化器中。
     • 记录已添加的边，避免重复（sInsertedEdges）。
4. 步骤4：添加其他主要类型的边（跟踪时形成的边、原始闭环边、高共视边）
   • 遍历地图中的所有关键帧 (vpKFs)：
     • 对于当前遍历到的关键帧 $K_i$：
       • 获取其逆位姿 $S_{wi}$ (从NonCorrectedSim3或vScw获取，优先使用未经过Sim(3)传播调整过的位姿)。
       • 步骤4.1：添加生成树的边（父子连接）
         • 获取 $K_i$ 的父关键帧 $K_p$ (在生成树中的父节点)。
         • 如果存在父关键帧：
           • 获取父关键帧 $K_p$ 的位姿 $S_{pw}$。
           • 计算相对位姿 $S_{pi} = S_{pw} \cdot S_{wi}$ 作为边的测量值。
           • 创建 g2o::EdgeSim3 边连接 $K_i$ 和 $K_p$，设置测量值和信息矩阵（通常为单位阵）。
           • 添加到优化器。
       • 步骤4.2：添加原始闭环连接边
         • 获取与 $K_i$ 形成闭环关系的关键帧集合 (sLoopEdges)。
         • 遍历这些闭环连接的关键帧 $K_l$：
           • 为避免重复添加，通常只处理 $K_l$ 的ID小于 $K_i$ 的ID的情况。
           • 获取 $K_l$ 的位姿 $S_{lw}$。
           • 计算相对位姿 $S_{li} = S_{lw} \cdot S_{wi}$ 作为边的测量值。
           • 创建 g2o::EdgeSim3 边连接 $K_i$ 和 $K_l$，设置测量值和信息矩阵。
           • 添加到优化器。
       • 步骤4.3：添加高共视程度的连接边
         • 获取与 $K_i$ 共视地图点超过阈值 (minFeat，如100) 的关键帧集合 (vpConnectedKFs)。
         • 遍历这些共视关键帧 $K_n$：
           • 进行一些检查避免重复添加：$K_n$ 不是 $K_i$ 的父关键帧， $K_i$ 不是 $K_n$ 的父关键帧，它们之间不构成已添加的闭环边，并且 $K_n$ 的ID小于 $K_i$ 的ID。
           • 同时，确保这条边没有在步骤3中因为地图点调整而被添加过（通过查询 sInsertedEdges）。
           • 如果通过所有检查：
             • 获取 $K_n$ 的位姿 $S_{nw}$。
             • 计算相对位姿 $S_{ni} = S_{nw} \cdot S_{wi}$ 作为边的测量值。
             • 创建 g2o::EdgeSim3 边连接 $K_i$ 和 $K_n$，设置测量值和信息矩阵。
             • 添加到优化器。
5. 步骤5：执行优化
   • 调用 optimizer.initializeOptimization() 来初始化优化过程（例如，构建雅可比矩阵结构）。
   • 调用 optimizer.optimize(N) 来执行N次迭代的优化（例如，N=20）。优化器会调整顶点的估计值（关键帧位姿）以最小化所有边的误差项之和。
6. 步骤6：更新关键帧位姿到地图中
   • 在更新地图数据前，通常会上锁（unique_lock<mutex> lock(pMap->mMutexMapUpdate))，以防止多线程冲突。
   • 遍历所有关键帧。
   • 对于每个关键帧 $K_i$：
     • 从优化器中获取其对应的顶点 VSim3 = static_cast<g2o::VertexSim3Expmap*>(optimizer.vertex(nIDi))。
     • 获取优化后的 Sim(3) 位姿估计 CorrectedSiw = VSim3->estimate()。
     • 将优化后的位姿（可能需要从Sim(3)转换回SE(3)，即如果尺度被优化了，需要除以尺度因子得到真实平移）更新到关键帧对象中（pKFi->SetPose(Tiw)）。
     • 同时，可以将优化后的逆位姿 $S_{wc}$ 存储起来（vCorrectedSwc）。
7. 步骤7：根据参考帧优化前后的相对关系调整地图点的位置
   • 这一步非常重要。由于本次优化只直接调整了关键帧的位姿，而没有直接优化地图点。因此，在关键帧位姿更新后，需要遍历所有地图点。
   • 对于每个地图点，它都有一个参考关键帧。根据其参考关键帧在优化前后的位姿变化（相对变换），来调整该地图点在世界坐标系下的三维坐标，以保持地图点与观测到它的关键帧之间的几何关系的一致性。这个过程在书中的后续代码或者其他模块中实现，但逻辑上是本质图优化后的一个必要步骤。

通过以上七个步骤，ORB-SLAM2能够在检测到闭环后，通过本质图优化有效地进行一次全局的位姿校正，从而显著提升整个SLAM系统的定位精度和地图的一致性。